 There are four components to an options price: underlying contract price, intrinsic value ( determined by strike price), time value (time remaining until expiration) and volatility. (A fifth element, interest rates, also can affect option prices, but for our purposes is unimportant.)
There are four components to an options price: underlying contract price, intrinsic value ( determined by strike price), time value (time remaining until expiration) and volatility. (A fifth element, interest rates, also can affect option prices, but for our purposes is unimportant.)
Intrinsic value refers to the amount an option is in-the-money. For example, with Eurodollar futures at 95.55, a 95.00 call has an intrinsic value of .55. The more an option is in the money, the greater its intrinsic value. At-the-money and out-of-the-money options have no intrinsic value.
Options are referred to as "wasting" assets because their value decreases over time until it reaches zero at expiration, a process called time decay. Time value refers to the part of an option's price that reflects the time left until expiration. The more distance an option's expiration date, the greater the premium because of the uncertainty of projecting prices further into the future.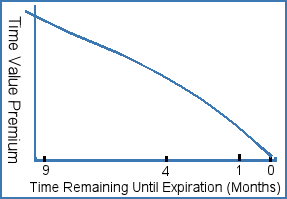
Considering two equivalent call options. Let's say for example, that with May corn futures at 232 1/4, July corn futures at 236 1/4 and 10 days left until May corn options expire, a May 230 call might cost 2 3/8 while a July 234 call costs 6 1/2, even though they are equally in-the-money.
Volatility, perhaps the most important and most widely ignored aspect of options, refers tot he range and rate of price movement of the underlying contract. The "choppier" the market, the higher the price that will be paid for this unstability in the form of higher option premiums.
Volatility usually is expressed as a percentage, and is comparable to the standard deviation of a contract. Higher volatility means higher premiums. Lower volatility means lower premiums. A trader familiar with the volatility history of a contract can gauge whether volatility at a given time is relatively high or low, and can profit from fluctuations in volatility that will in turn increase or decrease option premium.
The Black-Scholes price model, first introduced by Fischer Black and Myron Scholes in 1973, is the most popular theoretical options pricing model largely because it was the first relatively straightforward arithmetic method for determining a fair value for options.
Part 2 will be posted tomorrow, so stay tuned!
Best,
The MarketClub Team


